最適化問題で勾配法やニュートン法の基礎になる曲面と曲線の説明をします。
これを理解しておかなければ、最適化問題を理解することが出来ないので、しっかり勉強しましょう
曲線の法線ベクトル

上のような曲線に接する接するベクトルを考えます。曲線の内側・外側・曲線上ではf(x,y)の値はそれぞれ下のようになります。

この曲線上の2点 \(f(\bar{x},\bar{y}), f(\bar{x}+\Delta{x},\bar{y}+\Delta{x})\)について考えます。曲線上にあるので、以下の式が成り立ちます
\(f(\bar{x},\bar{y})=0, f(\bar{x}+\Delta{x},\bar{y}+\Delta{x})=0\)
第2式をテイラー展開すると下のようになります。
\(f(\bar{x}+\Delta{x},\bar{y}+\Delta{x}) = f(\bar{x},\bar{y}) + \dfrac{\partial{\bar{f}}}{\partial{{x}}}\Delta{x} + \dfrac{\partial{\bar{f}}}{\partial{{y}}}\Delta{y} \)+・・・・ =0
となります。ここから、ベクトル\( \nabla{f} ,\Delta{x}\)を下のように定義します。
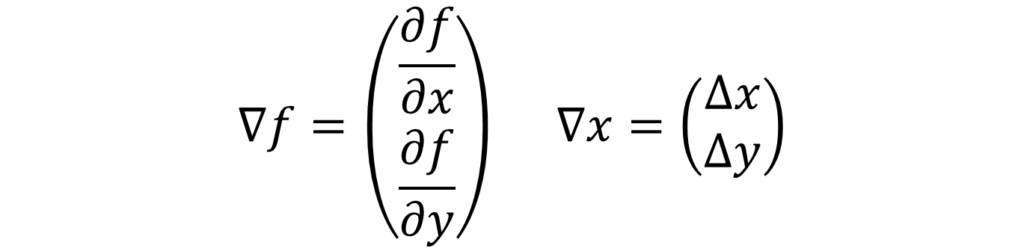
上のように定義すると、先ほどの式は次のようになります。
\(f(\bar{x}+\Delta{x},\bar{y}+\Delta{x}) =(\nabla{\bar{f}},\Delta{x}) +\)・・・=0
\(\nabla{\bar{f}}\)は\({\nabla{f}}\)の\((\bar{x},\bar{y})\)での値を意味すします。
この\(\nabla{\bar{f}}\)は曲線の法線ベクトルになります。定理にすると
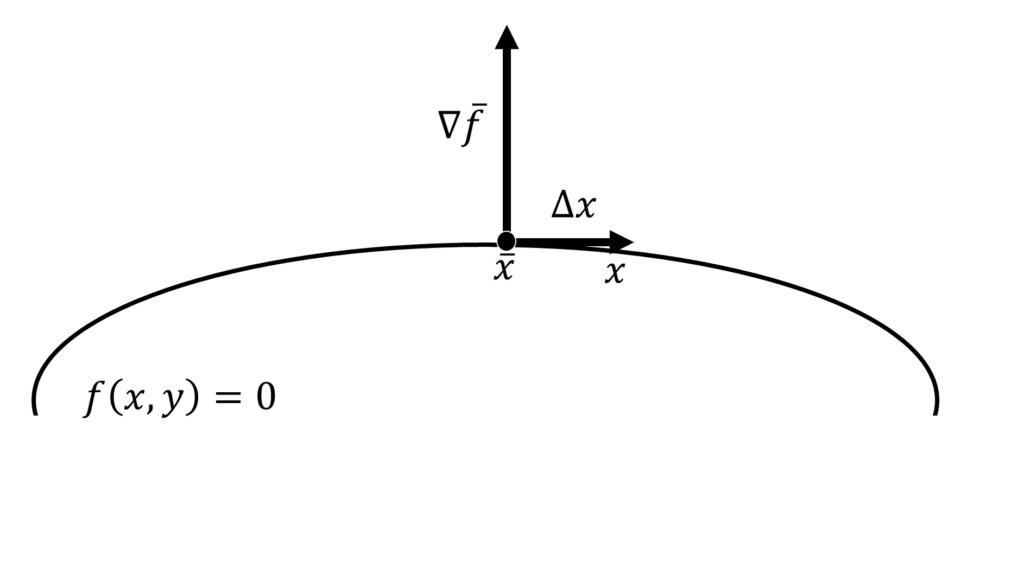
曲線\(f(x,y) =0\)の点\((x,y)\)における法線ベクトルは\(\nabla{f}\)である
曲線の接線
曲面の法線ベクトルに対する法線ベクトルを考えます。つまり、下図の赤線のベクトルを考えます。

この赤線が、曲線の上のを通るとき、曲線の接線になります。
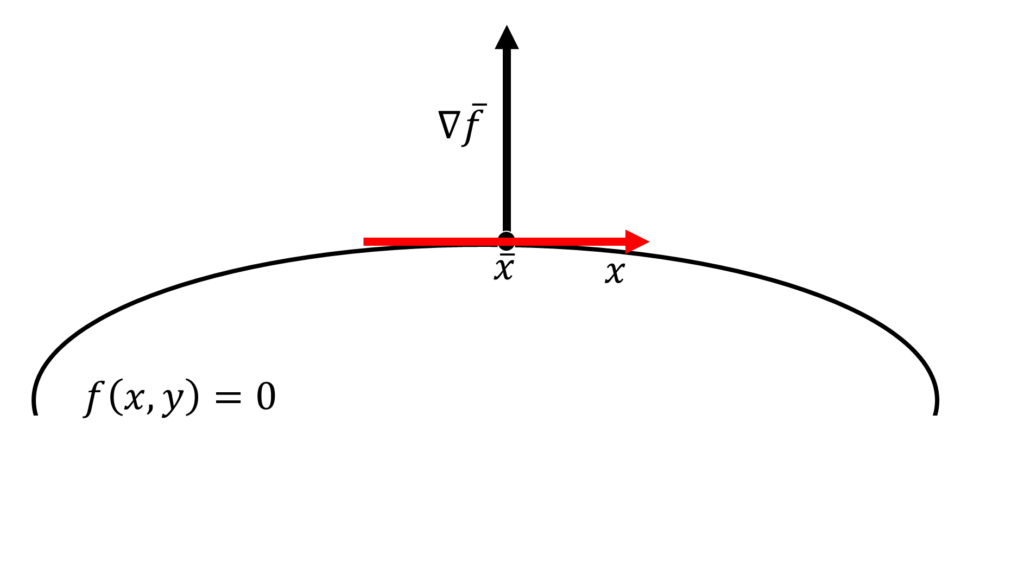
曲線の接線を求める公式は下のようになります。
点\(f(\bar{x},\bar{y})\)における曲線\(f( x,y) = 0\)の接線
\( \dfrac{\partial{\bar{f}}}{\partial{{x}}}(x – \bar{x})+ \dfrac{\partial{\bar{f}}}{\partial{{y}}}(y – \bar{y}) \) = 0
例として、放物線\(y=2x^2 + 3x – 1 \)の点\(1,4)\)における接線を求めてみます。
法線ベクトルは\(\nabla{f}\)で求められるので、放物線の法線ベクトルは下のようになります。
partial{\bar{f}}}{\partial{{x} = -4x -3 = -7 , partial{\bar{f}}}{\partial{{x} = 1
となり\( \begin{pmatrix} -7 \\ 1 \end{pmatrix}\)となります。これを公式に当てはめると
\( -7(x – 1) + (y -4) \)
\(y = 7x-3 \)
となり、接線は\(y = 7x-3 \)であることが分かります。
曲面の場合
曲面は基本的に、曲線にz軸が増えたものになります。
曲面\(f(x,y,z) =0\)の法線ベクトルは曲線と同じく以下のようになります。
曲面\(f(x,y,z) =0\)の点\((x,y,z)\)における法線ベクトルは\(\nabla{f}\)である
曲面の接面は以下のように求められます。
点\(f(\bar{x},\bar{y},\bar{z})\)における曲線\(f( x,y,z) = 0\)の接線
\( \dfrac{\partial{\bar{f}}}{\partial{{x}}}(x – \bar{x})+ \dfrac{\partial{\bar{f}}}{\partial{{y}}}(y – \bar{y})+\dfrac{\partial{\bar{f}}}{\partial{{z}}}(z – \bar{z}) \) = 0



コメント